Is there art in number?
SquareCirclez Mathematics, learning, computing, travel - and whatever...
- The Ultimate Guide to AI Math Solvers: Boosting Your Math Skills with Technologyby Casey Allen on February 6, 2025 at 4:37 am
The Ultimate Guide to AI Math Solvers: Boosting Your Math Skills with Technology Introduction to AI Math Solvers Mathematics has always been a subject that challenges students, often requiring extra practice and assistance to master. With the rapid advancements in technology, Artificial Intelligence (AI) has stepped in to bridge the gap, offering innovative solutions that Related posts: 5 Best Free Math Problem Solvers Math problems allow students to learn new concepts and strengthen... Math Homework Help: A Guide to the Best AI Math Solver of 2025 About a quarter of the average college student's courseload is... Solutions: A Guide to Problem Solving Review: Paperback This book is about general problem solving ('in... 21st century math skills A reader asks for advice on 21st century skills and...
- Math Homework Help: A Guide to the Best AI Math Solver of 2025by Casey Allen on December 1, 2024 at 4:20 am
About a quarter of the average college student's courseload is general education requirements. While these are graduation requirements, they also are usually time-wasters. They're challenging and stressful... but luckily, help is available. If you're looking for quick math homework help, an online AI math solver can bring your grades up quickly and effectively. Read on to Related posts: 5 Best Free Math Problem Solvers Math problems allow students to learn new concepts and strengthen... My dilemma - ethical math help Is there a difference between paying someone to do... Buyer’s Guide: TI-84 Graphing Calculator Math classes can be daunting. From a young age, I... Curriculum Webs - more homework needed "Weaving the Web into Teaching and Learning" Cunningham, C and...
- 5 Best Free Math Problem Solversby Casey Allen on June 6, 2023 at 3:43 am
Math problems allow students to learn new concepts and strengthen problem-solving skills. But many learners feel confused or frustrated if they can’t find the correct solution. A math problem solver is a handy tool that helps students doublecheck their work and identify errors. However, not all math problem solvers are created equal. Here are the Related posts: Microsoft Math 3.0 Review MS Math 3.0 is a well-designed computer-based math tool.... Free math software downloads Wanting to use some math software but find it’s too... GraphSketch.com - free online math grapher GraphSketch is a free offering that allows the user to... Context Free math-based art Context Free is software you can use to produce some...
- Reviewing Six Online Math Tutoring Services - What’s the Best?by Hugo Pegley on June 22, 2022 at 4:00 am
Math is an exciting field of study that can lead to a variety of exciting careers or research projects. But if you're a student having difficulty with the topic, you might be thinking about enrolling in an online math tutoring program. This is a great way for you to get assistance in a format and Related posts: How to Pick A Live Math Chat Tutoring Service If you’re looking for a live math tutor, you are... How Much Does an Online Math Tutor Cost? Across the world, math is the key to understanding many... Online Algebra Math Tutor Many private and public high schools and colleges require students... Best Online Calculus Math Tutor: How to Choose Calculus and math require tremendous background information, practice, and good...
- Picking the Best Online Precalculus Math Tutorby Hugo Pegley on June 22, 2022 at 3:55 am
Students who want to go on to study math, science, engineering, and other disciplines in college, usually find that their chosen college values some prior knowledge of calculus. An online precalculus math tutor could be the answer. High schools commonly offer precalculus courses in the 11th grade before introducing calculus in the 12th. Precalculus is Related posts: How Much Does an Online Math Tutor Cost? Across the world, math is the key to understanding many... Best Online Calculus Math Tutor: How to Choose Calculus and math require tremendous background information, practice, and good... Online Algebra Math Tutor Many private and public high schools and colleges require students... Reviewing Six Online Math Tutoring Services - What’s the Best? Math is an exciting field of study that can lead...
Surrey Mathematics Research Blog The blog on research in mathematics at the University of Surrey
- Paper of Gutowski, Saelim, and Wolf published in Classical and Quantum Gravityby Tom Bridges on January 30, 2026 at 5:50 pm
The paper “Extremal black holes from homotopy algebras“, co-authored by Jan Gutowski, Chettha Saelim, and Martin Wolf, was published today (30 January) in the journal “Classical and Quantum Gravity“. In this paper, the authors investigate the construction of all extremal black hole solutions to the Einstein equation for a given near-horizon geometry, employing the homotopy
- Paper of Kalinowski, Bridges, and Baresi presented at the AIAA Scitech in Orlandoby Tom Bridges on January 20, 2026 at 6:14 pm
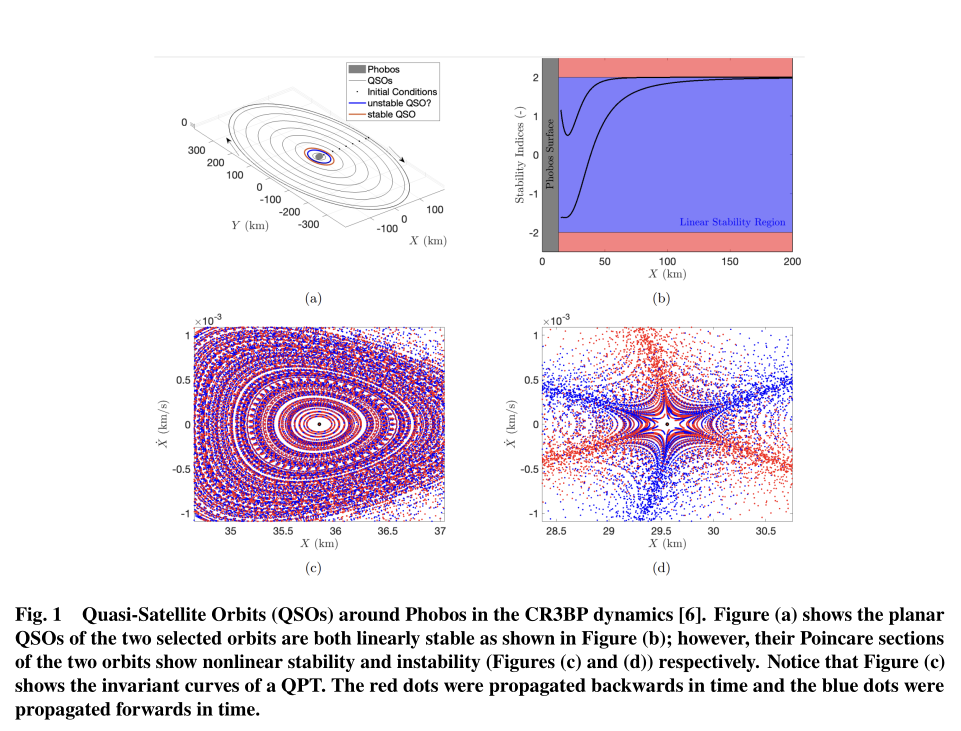
The paper “High Order Continuation With Automatic Bifurcation Identification in the Circular Restricted Three Body Problem“, co-authored by Wojciech Kalinowski (Surrey Space Centre), Tom Bridges, and Nicola Baresi (Surrey Space Centre) was presented and published at the American Institute of Aeronautics and Astronautics Scitech 2026 Forum, held in Orlando, Florida 12-16 January. Wojciech presented the
- Paper of Martin Wolf on non-Abelian gerbes published in Journal of Physics Aby Tom Bridges on January 20, 2026 at 3:10 pm
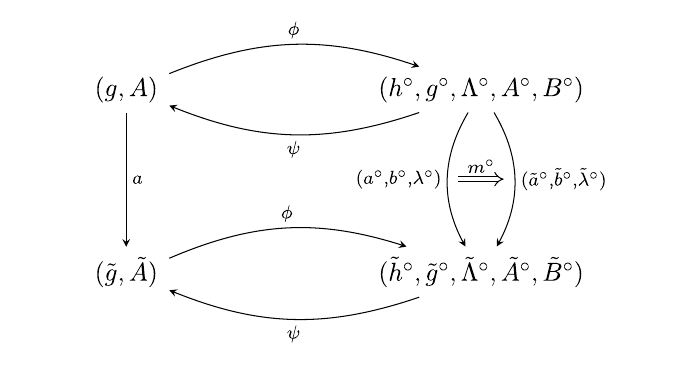
The paper “Explicit non-Abelian gerbes with connections“, co-authored by Dominik Rist (Heriot-Watt & Maxwell Institute), Christian Saemann (Heriot-Watt & Maxwell Institute), and Martin Wolf, has been published (open access) today (20 January) in the Journal of Physics A: Mathematical and Theoretical (link here). A sketch of the paper is as follows. The authors define the
- Paper of Alessandro Torrielli accepted for publication in Physical Review Researchby Tom Bridges on January 19, 2026 at 5:47 pm
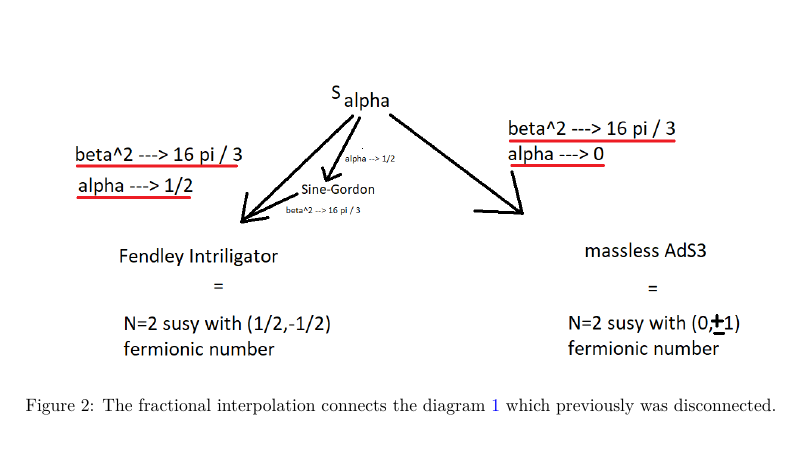
The paper “AdS3 integrability, Sine-Gordon and fractional supersymmetry“, with author Alessandro Torrielli, has been accepted for publication in Physical Review Research as a regular article. A final form preprint in available on the arXiv (link here). The massless S-matrix of the pure RR AdS3 X S3 X T4 theory is very similar but not quite
- Paper of Aravind Kumar Kamaraj published in Nature Portfolio Journal on Systems Biologyby Tom Bridges on January 15, 2026 at 5:17 pm
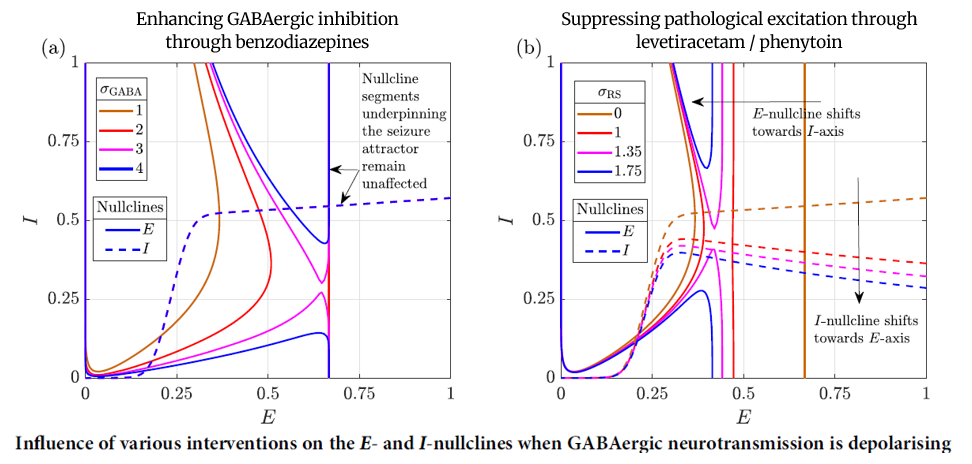
The paper “Modelling dysfunction-specific interventions for seizure termination in epilepsy”, co-authored by Aravind Kumar Kamaraj and Matthew Szuromi (Boston University, USA), has been published in the npj Systems Biology and Applications (link to published paper here). The authors use a parsimonious two-dimensional neural mass model to study why first-line treatments fail to terminate seizures in a subset
Mathematics – Wolfram Blog News, Views and Insights from Wolfram
- Learning Decision Process Theory with a Wolfram Language Toolkitby Gerald H. Thomas on August 22, 2025 at 7:30 pm
In our daily lives, individuals, corporations and societies are constantly involved in making decisions. We hope to make optimal choices, especially when faced with recurrent decision processes. Thus we care about why and how our decision processes change over time. As a practicing engineer and an instructor in higher education, it is my opinion that
- What’s Up with Daylight Saving Time? A Brief History and Analysis with Wolfram Languageby Nick Lariviere on March 5, 2025 at 5:12 pm
In the next few days, most people in the United States, Canada, Cuba, Haiti and some parts of Mexico will be transitioning from “standard” (or winter) time to “daylight” (or summer) time. This semiannual tradition has been the source of desynchronized alarm clocks, missed appointments and headaches for parents trying to get kids to bed at the right time since 1908, but why exactly do we fiddle with the clocks two times a year?
- A Whole New Ball Game: Game Theory in Wolfram Language 14.2by Marc Vicuna on February 25, 2025 at 6:17 pm
Do you want to make optimal decisions against competition? Do you want to analyze competitive contexts and predict outcomes of competitive events? Do you need to elaborate strategies and plans against adversity and test the effectiveness of those strategies? Or are you simply an undergraduate student struggling to cope with a required course on game
- Master the Basics of Laplace Transforms in Just 15 Lessons with Wolfram Languageby Juan Ortiz on February 5, 2025 at 8:30 pm
The Laplace transform provides effective and easy means for solving many problems that arise in the fields of science and engineering. It is one of the main tools available for solving differential equations. For most of us, the first time we see it is in an introductory differential equations course. Wolfram Language provides an ideal
- Learn Complex Analysis Today with Wolfram Languageby Marco Saragnese on October 15, 2024 at 3:44 pm
Complex analysis is a versatile tool that is used extensively in science, engineering and other fields. It is also a beautiful topic in and of itself. Hence, a course in complex analysis is a standard part of the curriculum for physics and engineering students and a stepping stone for more advanced topics in mathematics. Wolfram
- Hypergeometric Functions: From Euler to Appell and Beyondby Tigran Ishkhanyan on January 25, 2024 at 5:35 pm
Hypergeometric series appeared in the mid-seventeenth century; since then, they have played an important role in the development of mathematical and physical theories. Most of the elementary and special functions are members of the large hypergeometric class. Hypergeometric functions have been a part of Wolfram Language since Version 1.0. The following plot shows the implementation
- Get Down to Business with Finite Mathematics in Wolfram Languageby John McNally on December 22, 2023 at 3:41 pm
“There is every reason to expect that the various social sciences will serve as incentives for the development of great new branches of mathematics and that some day the theoretical social scientist will have to know more mathematics than the physicist needs to know today.” —John G. Kemeny, first author of the original textbook on
- Don’t Be Discreet and Learn Discrete Mathematics with Wolfram Languageby Marc Vicuna on November 29, 2023 at 6:00 pm
“The spread of computers and the internet will put jobs in two categories. People who tell computers what to do, and people who are told by computers what to do.” — Marc Andreessen, inventor of the Netscape browser How is data organized in databases? Why are some computer programs faster than others? How can algorithms
- Learn Multivariable Calculus through Incredible Visualizations with Wolfram Languageby Tim McDevitt on November 6, 2023 at 3:57 pm
Multivariable calculus extends calculus concepts to functions of several variables and is an essential tool for modeling and regression analysis in economics, engineering, data science and other fields. Learning multivariable calculus is also the first step toward advanced calculus and follows single-variable calculus courses. Wolfram Language provides world-class functionality for the computation and visualization of